सरल समीकरण (गणितीय समीकरण) परिभाषा, उदाहरण, समीकरण, एवं हल इत्यादि,

 सरल समीकरण यह     समीकरण का ही स्वरूप है सरल समीकरण मे  जोड़ (+) ,घटना (-), गुना (×) , भाग  (÷) , जैसे  आदि घटक होते है।  सरल  समीकरण  को हल करने के कुछ नियम  होते है। जिनके आधार पर चर का मांन ज्ञात किया जाता है। सरल  समीकरण को इंग्लिश मे " EQUATION " कहते है । सरल समीकरण  मे दो पक्ष होते है। एक  "दाया पक्ष" और दुसरा "बाया पक्ष " होता है।  दाया पक्ष  को इंग्लिश में " (RHS) "और बाया पक्ष  को इंग्लिश  " (LHS) " कहते है ।   समीकरण के हल को इंग्लिश मे " SOLUTION " कहते है।  समीकरण के दोनों पक्षों के मध्य बराबर ( = ) / " EQUAL " का चिन्ह होता है। जो दाया पक्ष और बाया पक्ष के बीच समानता को  दर्शाता है। 

सरल समीकरण मे " चर "का महत्वपूर्ण भूमिका होतीं है । चर को इंग्लिश मे " VARIABLE " कहते है । चर का मान समीकरण को हल करके ही ज्ञात किया जाता है। चर का मान अस्थिर होता है । जो बदलता रहता है । समीकरण एक प्रकार का व्यंजक ही है। जो जोड़,  घटाना, गुणा ,भाग, बराबर,  एवं संख्याओं का मिश्रण है । व्यंजक को इंग्लिश मे  " EXPRESSION "कहते हैं ।  व्यंजक द्वार ही चर के मान की पुष्टि की जाती है और समीकरण का हल  है या नही  यह निर्धारित किया जाता है। व्यंजक लिखते समय समीकरण के मध्य बराबर का चिन्ह होता है। यदि बराबर का चिन्ह नही हो तो  वह समीकरण नही  होता है । 

उदाहरण

 यह समीकरण  है ।, 

   2x + 6 = 14

   2x = 14 - 6

    2x = 8

    X=8/2

    X = 4

यह समीकरण नही है। 

1 ) 2 - 3 × 4 ÷ 2 < 8

2 )  2 + 3 × 4 > 5

व्यंजक मे कम से कम एक चर होना आवश्यक है। समीकरण मुख्यत चर पर ही निर्भर होता है । 

चर  इंग्लिश  वर्णमाला  के अक्षर a,,b,c, d,e, ............... x, y, z, इत्यादि के रूप मे ले लिया जाता हैं। 

उदाहरण ,

 यदि किसी अज्ञात संख्या का मान ज्ञात न होतो  उसे चर के  रूप मे मानकर हल  करके मान ज्ञात किया जाता हैं। 

TYPE - 1

1)  मानो वह संख्या x  है। 

2)  मानो वह संख्या y है। 

3) मानो वह संख्या  p है। 

4)  मानो वह संख्या  a है। 

5) मानो वह संख्या  b है। 

TYPE - 2

उदाहरण, 

यदि कोई अज्ञात संख्या किसी संख्या की गुना हो  तो उसे लिखने का स्वरूप निम्नलिखित प्रकार से है। 

1) मानो वह संख्या X  है और वह 5 की गुना है। 

Ans - x × 5 = 5x

2)  मानो वह संख्या y है और वह 6 की गुना है। 

Ans -  y × 6 = 6y

3) मानो वह संख्या a  है और वह 7 की गुना है। 

Ans - a × 7 = 7a

4) मानो वह संख्या q  है और वह 8 की गुना है। 

Ans - q × 8 = 8q

5) मानो वह संख्या r  है और वह 9 की गुना है। 

Ans - r× 9 = 9r

TYPE - 3

उदाहरण , 

यदि कोई अज्ञात संख्या किसी संख्या की गुना हो और किसी संख्या से अधिक एवं कम हो तो उसे लिखने का स्वरूप निम्नलिखित प्रकार से है। 

1) यदि कोई संख्या स्वय के 3 गुना से 5 अधिक हो तो गणितीय स्वरूप मे लिखो 

Ans -  मानो वह संख्या x है तथा स्वय के 3 गुना से 5 अधिक            है।  

         समीकरण -:   x  × 3 + 5 =  3x + 5

2) यदि कोई संख्या स्वय के 5 गुना से 4 अधिक हो तो गणितीय स्वरूप मे लिखो 

Ans - मानो वह संख्या m है तथा स्वय के 5 गुना से 4 अधिक है।  

        समीकरण -: m × 5 + 4 = 5m + 4

3) यदि कोई संख्या स्वय के 7 गुना से 4 कम हो तो गणितीय स्वरूप मे लिखो 

Ans - मानो वह संख्या p है तथा स्वय के 7 गुना से 4 कम है।  

        समीकरण -: p × 7 - 4 = 7p - 4

4) यदि कोई संख्या स्वय के 5 गुना से 3 कम हो तो गणितीय स्वरूप मे लिखो 

Ans - मानो वह संख्या q है तथा स्वय के 5 गुना से 3 कम है।  

       समीकरण -: q × 5 - 3 = 5q - 3

5) यदि कोई संख्या स्वय के 2 गुना से 10 कम हो तो गणितीय स्वरूप मे लिखो 

Ans - मानो वह संख्या y है तथा स्वय के 2 गुना से 10 कम है।  

       समीकरण -: y × 2 - 10 = 2y - 10

TYPE - 4

उदाहरण , 

यदि कोई अज्ञात संख्या किसी संख्या की गुना हो और किसी संख्या से अधिक एवं कम हो तथा उनका योगफल उसे लिखने का स्वरूप निम्नलिखित प्रकार से है। 

1) यदि कोई संख्या स्वय के 2 गुना से 10 घटाने पर प्राप्त 20  होता है तो गणितीय समीकरण स्वरूप मे लिखो । 

Ans - मानो वह संख्या y है  तथा स्वय के 2 गुना से 10  घटाने पर प्राप्त होता है तो गणितीय समीकरण लिखो

     y × 2 - 10 = 20

     2y - 10 = 20

2) यदि कोई संख्या स्वय के 2 गुना से 5 अधिक है तथा उनका योगफल 29  प्राप्त होता है तो गणितीय समीकरण  लिखो । 

Ans - मानो वह संख्या x है तथा स्वय के 4 गुना से 5 अधिक है तथा उनका योगफल 29 तो गणितीय समीकरण लिखो। 

    x × 4 +5 = 2

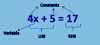
   4x + 5 = 29 

3) यदि कोई संख्या स्वय के 5 गुना से 7 अधिक है तथा उनका योगफल 27 प्राप्त होता है तो गणितीय समीकरण लिखो । 

Ans - मानो वह संख्या y है तथा स्वय के 5 गुना से 7 अधिक है तथा उनका योगफल 27 तो गणितीय समीकरण लिखो। 

    y × 5 +7 = 27

    5y + 7 = 27 

उदाहरण , 

निम्नलिखित हल कीजिये। 

4) यदि कोई संख्या स्वय के 3 गुना से 3 अधिक है तथा उनका योगफल 12 प्राप्त होता है तो गणितीय समीकरण  लिखो । 

5) यदि कोई संख्या स्वय के 7 गुना से 3 घटाने पर प्राप्त 18 होता है तो गणितीय समीकरण स्वरूप मे लिखो । 

6) यदि कोई संख्या स्वय के 6 गुना से 7 अधिक है तथा उनका योगफल 25 प्राप्त होता है तो गणितीय समीकरण लिखो । 

7) यदि कोई संख्या स्वय के 4 गुना से 5 घटाने पर प्राप्त 28  होता है तो गणितीय समीकरण स्वरूप मे लिखो । 

8) यदि कोई संख्या स्वय के 2 गुना से 6 घटाने पर प्राप्त 18  होता है तो गणितीय समीकरण स्वरूप मे लिखो । 

9) यदि कोई संख्या स्वय के 8 गुना से 3 घटाने पर प्राप्त 29  होता है तो गणितीय समीकरण स्वरूप मे लिखो । 

10) यदि कोई संख्या स्वय के 10 गुना से 3 अधिक है तथा उनका योगफल 33 प्राप्त होता है तो गणितीय समीकरण लिखो । 

TYPE -5

निम्नलिखित प्रश्न को हल कीजिये । 

1) यदि   x + 3 = 8 होतो  x  का  मान ज्ञात कीजिये । 

Ans - :    x + 3 = 8 

               x = 8 - 3

               x = 5

2) यदि  x - 5 = 12 होतो x का मान ज्ञात कीजिये ।

Ans - :    x - 5 = 12 

               x = 12 +5

               x = 17

3) यदि   m - 4 = 8 होतो  m  का  मान ज्ञात कीजिये ।

4) यदि   p + 6 = 12 होतो  p  का  मान ज्ञात कीजिये ।

5) यदि   a - 3 = 5 होतो  a  का  मान ज्ञात कीजिये ।

6) यदि k - 6 = 15 होतो k का मान ज्ञात कीजिये ।

7) यदि   a + 8 = 15 होतो  a  का  मान ज्ञात कीजिये ।

8) यदि   x + 6 = 25 होतो  x  का  मान ज्ञात कीजिये ।

9) यदि  m + 6 = 13 होतो m का मान ज्ञात कीजिये ।

10) यदि m - 9 = 18 होतो m का मान ज्ञात कीजिये ।

TYPE -5

निम्नलिखित प्रश्न के मान समीकरण के हल है या नही । 

 1)  x + 3 = 8        x = 5  समीकरण का हल है या नही ? 

Ans -          x + 3 = 8    

    x = 5   समीकरण मे  रखने पर

बाया पक्ष = x + 3

             = 5 + 3

             = 8

बाया पक्ष = दाया पक्ष 

x = 5 समीकरण का हल है। 

2)   2x + 6 = 12     x = 3 समीकरण का हल है या नही ?

3) 4x + 3 = 19      x = 4 समीकरण का हल है या नही ?

4) 2x - 3 = 5         x = 2 समीकरण का हल है या नही ?

5) 5x  - 6 = 8        x = 1 समीकरण का हल है या नही ?

6)   x + 6 = 8        x = 3  समीकरण का हल है या नही ? 

7)   x + 7 = 12     x = 5  समीकरण का हल है या नही ? 

8)   x + 8 = 12     x = 4  समीकरण का हल है या नही ? 

9)   5x + 6 = 16   x = 2  समीकरण का हल है या नही ? 

10)   x + 3 = 5     x = 2  समीकरण का हल है या नही ?